论文:
Tse-Yu
Yeh and Yale N. Patt. A Comparison of Dynamic Branch Predictors that use
Two Levels of Branch History. ISCA 1993.
感觉这篇文章讲得太简略了,建议先看一下上面那篇1992年的文章。
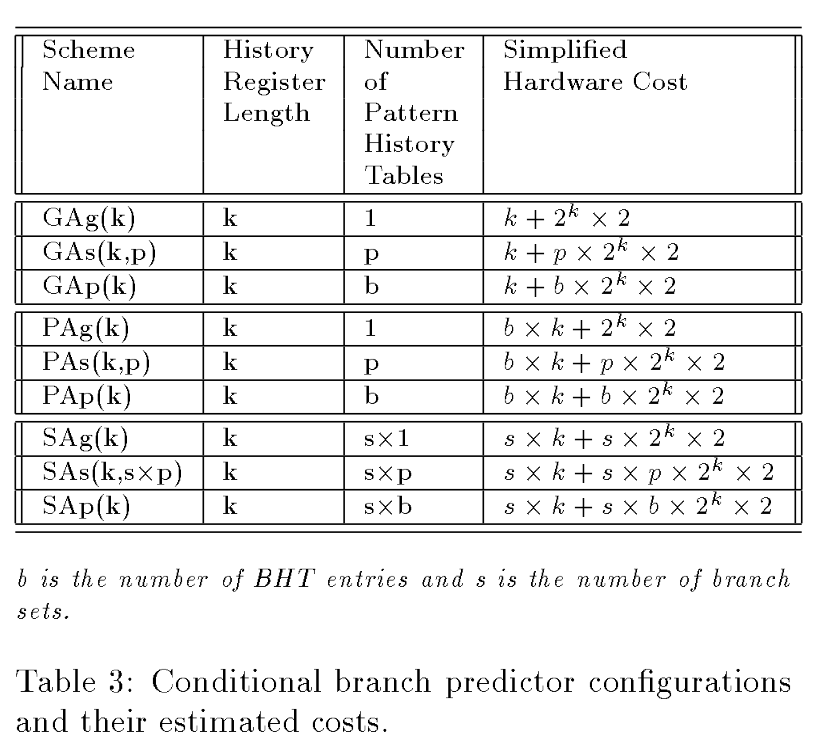
预测器分为两层,第一层记录前k个分支执行的历史,如果是taken就是1,如果是not taken就是0。根据"前k个分支"的定义,分为三个scheme。对于global history scheme,第一层就记录全局的前k个分支的执行历史,对于per-address history scheme,第一层就记录每个分支的前面k次的执行历史,对于per-set history scheme,第一层就记录每个组中的分支的前面k次的执行历史。分支所在的组可以由分支类型决定,也可以由分支的地址决定。
将前k个分支执行的结果的取值看作一个pattern,第二层就是用来决定在每个parttern下,应该怎么预测的。一般来讲,第二层由很多2-bit
FSM组成(来源:https://en.wikipedia.org/wiki/Branch_predictor)。跟第一层一样,第二层也可以分成三类:global,
per-address, per-set。Global时,第二层就是一个长度为
第一层和第二层各三种结构,一共有九种。
第一层里的分支执行历史的更新是speculative的,即拿到预测结果之后直接假装它是对的,来更新这个执行历史,如果有必要再修正,这样预测下一个分支的时候才能找到比较正确的第二层的2-bit FSM。但是第二层里的2-bit FSM的更新是拿到真正的分支执行的结果之后,才更新的(预测的时候要把pattern记下来)。
Global history scheme对integer programs来说表现比较好,因为这类程序里有很多if-then-else的逻辑,这种逻辑里,各条分支语句一般是有联系的。而global history scheme就很擅长发现这种分支语句之间的联系。但是不同的分支可能会共享同一个pattern,然后就跑到同一个pattern history table里了,所以要达到好的效果,要追踪更长的全局历史(即更长的pattern,更长的pattern history table),或者弄更多的pattern history table(毕竟不可能每个分支或者set都配一个pattern history table,应该是用类似于哈希表的方式做的,那就增加哈希表的长度)。
Per-address history scheme比较适合floating point programs,因为这类程序里循环比较多,分支之间比较独立,分支本身的周期性比较强。我觉得Per-address history scheme是基本不能发现指令之间的关系的,因为虽然在PAg(即第一层是per-address,第二层是global)和PAs(即第一层是per-address,第二层是per-set)中,很多个分支可能会共用一个pattern history table,但是下标用的是这个分支自己的执行历史,也就是pattern,这种关系与其说是体现了指令之间的关系,不如说是一种类似于哈希冲突的有害的关系。
Per-set history scheme结合了前两者的优点,但是要达到好的效果,其成本很高。我觉得SAp(第一层是per-set,第二层是per-address)和PAs(第一层是per-address,第二层是per-set)是不同的,因为SAp中,是先拿到了所处set的pattern,即执行历史,然后再到这个分支对应的pattern history table里拿2-bit FSM的。而PAs中,用的历史是这个分支的历史。
总的来说,如果要求开销低,那么PAs最好,8Kb时能达到96.3%的准确度,如果可以接受高开销,那么GAs最好,128Kb时能达到97%的准确度。
¶ 没看懂的地方
为什么Per-set history scheme里,好像每个set都有一个自己的pattern history
table?那SAs里,第二层的set是怎么定义的?