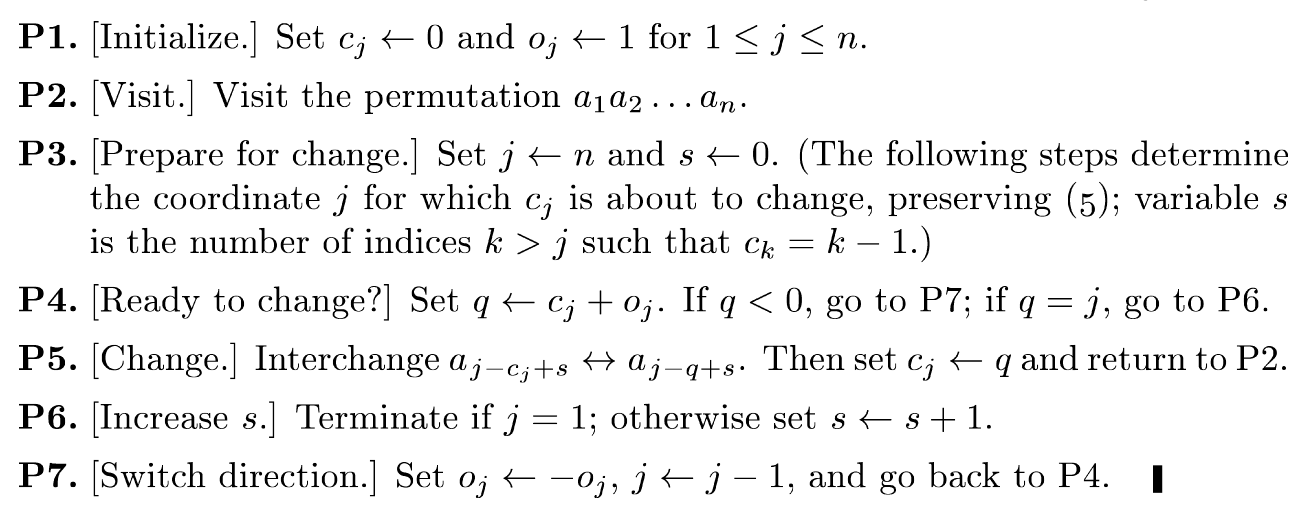# 思路

SJT算法就是给每个值一个方向，初始都向左（P1），然后从最大的值开始检查（P3），一直检查到最小的值，直到找到值，使得其方向上的下一个值小于它（P4），然后将其往那边移动一步（P5），然后继续从最大的值开始找（return to P2）。对于每个被检查的值，如果这个值的方向上的下一个值不小于它，就调转它的方向，然后继续检查次小的值。

这样为什么可以枚举到所有的排列呢？这实际上可以递归的证明。首先我们知道，n=1时，这样是可以做到枚举到所有排列的。然后我们假设对于n=N-1时，这样做可以做到枚举到所有的排列。然后我们要证明对于n=N时，这样做可以枚举到所有的排列。

首先，将N移动到最左边或者最右边之后，我们将1到(N-1)的子序列变换到下一个全排列，在算法中体现为继续检查次小值能不能移动。由假设可知，通过这种方式，子序列可以遍历到所有的全排列，所以我们只需要将N反向再穿插过去，就可以遍历到包含这个子序列的1到N的全排列了。

¶ P1

到是序列，是的右边小于的数的个数，是的方向，1表示向左，-1表示向右。刚开始，序列是，所以把都初始化为0，都初始化为1。

¶ P2

不知道干啥的

¶ P3

然后我们选定选择要移动的数字，一开始找最大的数字，也就是令。令表示的左边比大的数字的个数，那么的下标就是，可以形象地理解为，从的左边拿掉比小的个数字，然后再将个比大的数字插入到的左边。

¶ P4

因为我们的思路是先让大的走，而且不允许小的值把大的“挤走”，所以既然我们现在是要让走，说明大于的都走不动了，也就是说，比大的值中，向右走的必然全部集中在最右边，向左走的必然全部集中在最左边。因此，走的那个方向上如果有小于的值，那么该方向上的下一个值必然是小于的。

我们令，如果能走得动的话，这个实际上就是的新值。

如果，说明在向右走，且右边没有比它小的值了，也就是说走不动了。这时就跳转到P7，改变的方向，然后令，即继续检查下一个值能不能走得动。

如果，说明在向左走，且左边没有比小的值了，也就是说走不动了。这时跳转到P6，如果，说明所有值都走不动了，这时算法就结束了。否则，同样跳转到P7，改变的方向，然后继续检查下一个值。但是不同的是，对于下一个值，左边多了一个比它大的值，所以要加一。

如果，那么走得动，就跳转到P5，让它跟下一个值交换，把更新成，然后跳转到P2，继续从最大的数字开始检查能不能走得动。