量子计算机学习笔记

¶ qubit

经典的bit的状态空间为2，要么是0，要么是1。但是qubit可以同时是0和1，其状态空间可以看作是一个半径为1的球面，如下图Bloch sphere所示。

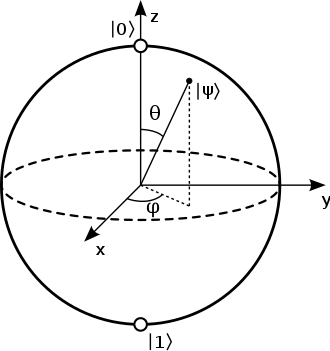
图片来源：https://en.wikipedia.org/wiki/Bloch_sphere

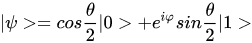
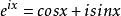
可见，与直觉不同，它有两个自由度。为了简化，将其记为下面的形式：

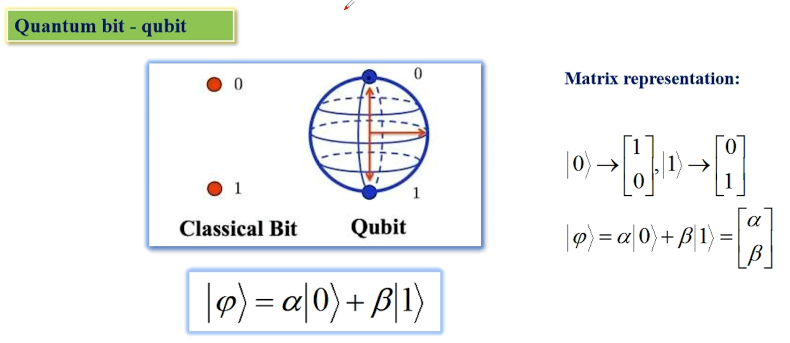
图片来源：http://www.asc-events.org/ASC20-21/Trainingcamp.php

如果进行观测，则量子比特会坍缩成经典bit：

可以看到，影响其坍缩到0还是1的概率的是，而不影响。但是有一些量子门可以利用来影响。

¶ 多qubit

有n(n>1)个qubit时，由于它们之间有量子纠缠，所以一个qubit的状态与另一个qubit的状态有关。这样，这些qubit的状态有2的n次方种，每种状态都有自己的概率。对这些qubit的操作都会作用到所有的状态上去。我认为可以理解成超级SIMD。

图片来源：http://www.asc-events.org/ASC20-21/Trainingcamp.php

图片来源：http://www.asc-events.org/ASC20-21/Trainingcamp.php

¶ 量子门

内容参考自：https://en.wikipedia.org/wiki/Quantum_logic_gate

对量子的操作以量子门的形式进行。量子门有的只操作一个qubit，有的操作多个qubit。

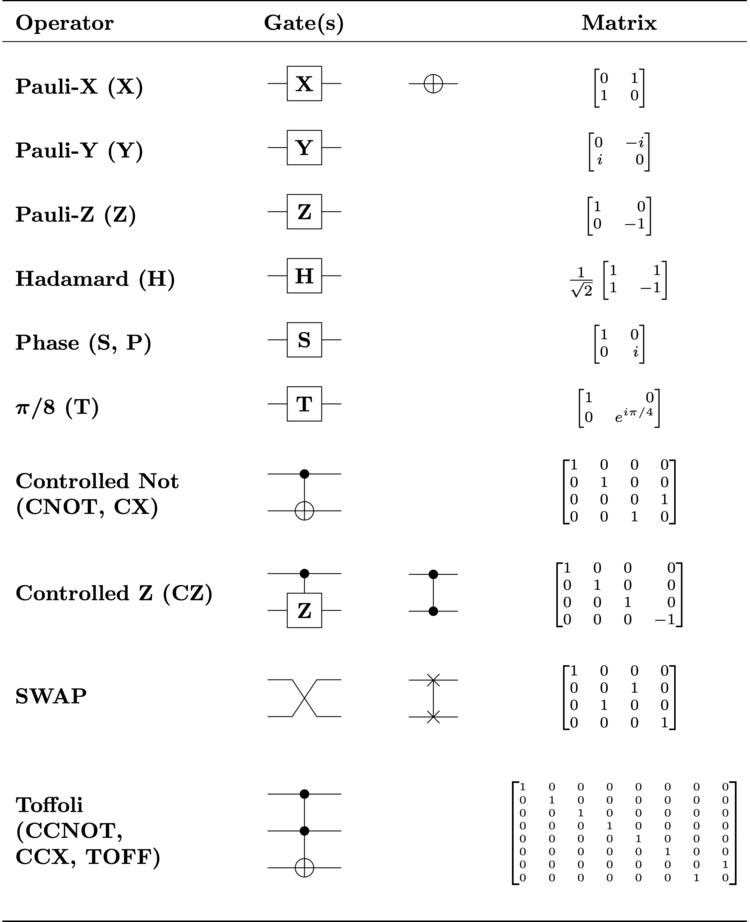
¶ 操作一个qubit的量子门

表示成矩阵就是

¶ Pauli-X (X)

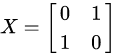
显然是交换其0和1的状态的概率。wiki上说是相当于绕x轴旋转180度，但是旋转之后变成了，变成了，代进式子发现是，而不是？？？

¶ Controlled Not (CNOT, CX)

相当于对于第一个qubit为1的情况，将第二个qubit的0和1反过来。